*Familiarization with discrete FFT
smallest_circle
 circle
circle
 smaller circle
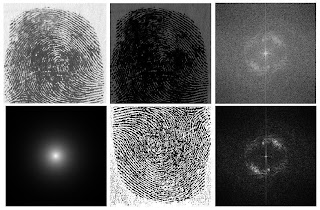
smaller circle  Image above(clockwise from top left): original image; FFT of image; shifted FFT of image; original image with FFT applied twice.
Image above(clockwise from top left): original image; FFT of image; shifted FFT of image; original image with FFT applied twice.
Using the code below resulted to the images above. When FFT is applied twice to an image, an image of the original image is produced. This maybe so for a centered circle but the difference can clearly be seen when the same procedure is done to an image not centered and non-uniform in shape. (Note: circle produced after applying FFT twice is a bit out of shape because it was scaled.)
I = imread('circle.bmp');
Igray = im2gray(I);
FIgray = fft2(Igray); //FIgray is complex
scf(1);
imshow(abs(FIgray),[]);
scf(2);
imshow(fftshift(abs(FIgray))), []);
scf(3);
imshow(abs(fft2(fft2(I))));
The code above was again used, and this time, the image of the letter A is now inverted after applying FFT twice. This happens because when FFT is used, the quadrants along the diagonals interchange.
 Image above(clockwise from top left): original image, FFT of image; image after applying FFT twice; shifted FFT of image.(The inverted image was scaled .)
Image above(clockwise from top left): original image, FFT of image; image after applying FFT twice; shifted FFT of image.(The inverted image was scaled .)
*Simulation of an imaging device
r=imread('C:\MyDocuments\AP186\circle.bmp');
a=imread('C:\MyDocuments\AP186\VIP.bmp');
rgray = im2gray(r);
agray = im2gray(a);
Fr = fftshift(rgray);//aperture is already in the Fourier Plane and need not be FFT'ed
Fa = fft2(agray);
FRA = Fr.*(Fa);
IRA = fft2(FRA); //inverse FFT
FImage = abs(IRA);
imshow(FImage, [ ]);
Using this code, the following images were produced:

Image above(clockwise from top left): original image; convolved image using circle image; convolved image using smaller_circle image; convolved image using smallest_circle image.
As we can see, as the circle being used gets smaller, the quality of the image becomes lesser.
*Template matching using correlation
r=imread('C:\MyDocuments\AP186\text.bmp');
a=imread('C:\MyDocuments\AP186\A.bmp');
rgray = im2gray(r);
agray = im2gray(a);
Fr = fftt2(rgray);
Fa = fft2(agray);
b = conj(Fr);
FRA = (Fa).*b;
IRA = fft2(FRA);
FImage= abs(IRA);
imshow(FImage, [ ]);
With this code, the originial image became unrecognizable. The texts in the image looked like letters A.

 *Edge detection using convolution integral
*Edge detection using convolution integral
pattern = [-1 -1 -1; 2 2 2; -1 -1 -1];
a=imread('C:\MyDocuments\AP186\VIP.bmp');
image = imcorrcoef(a, pattern);
imshow (image, []); 
Using the code, the following images were formed. The first image shows a horizontal pattern since the pattern used here is also horizontal. The second image used a vertical pattern hence the image of VIP followed that pattern. It's also the same with the 3rd image, this time a spot pattern was used.
Acknowledgements: Jorge Presto
Grade: 10/10 - because the activity was well done.






























 Grade: 6/10 - It was passed late.
Grade: 6/10 - It was passed late.



 Image above(clockwise from top left): original image; convolved image using circle image; convolved image using smaller_circle image; convolved image using smallest_circle image.
Image above(clockwise from top left): original image; convolved image using circle image; convolved image using smaller_circle image; convolved image using smallest_circle image.
 *Edge detection using convolution integral
*Edge detection using convolution integral


 Applying DFT will decompose the image to its sinusoidal components. Note that the Image should be in grayscale.
Applying DFT will decompose the image to its sinusoidal components. Note that the Image should be in grayscale.





